This article introduces several issues related to the problem of navigating multi-dimensional data spaces—large databases. It examines problems with trying to conform data to a single taxonomy and the limits of tree structures as navigational devices. It offers several alternative devices, and it notes the need to enable random, multi-variate filtering so that users may narrow and expand at will. It also introduces the concept of pivoting: narrowing along one path and turning (or pivoting) to expand along another path.
**Context**
Over the past 25 years we have come to expect digital information to be organized in hierarchies. File systems are tree structures: *C:\main\branch\subbranch\leaffile.doc*
The web, built on top of networked file systems, reinforced this form of navigation: *http://www.apple.com/ipod/features.html*
**Introduction to Tree Structures**
Tree structures begin with a root. They also have branches. Imagine this process repeated. A tree can be as deep (or tall) as you want. For our purposes, we will restrict our tree to only three levels. At the end of the branches are leaves. Imagine this process repeated any number of times. As wide (or broad) as you want.
**Limitations of Tree Structures**
Earlier, we saw that trees can be arbitrarily deep or wide. In practice, human perception has limits. Faced with many choices we may have difficulty comprehending them all. For example, many items at the same level in a menu may be difficult to parse.
George Miller’s famous paper, *The Magic Number 7, Plus or Minus 2: Limits on Our Capacity for Processing Information* and research on short-term memory suggest a rule-of-thumb for designers. It may be best to limit the number of choices in a list to 7. If you have more than 7, it may be time to create groups—to nest categories.
That suggests the following corollaries:
+ No more than 7 tabs
+ No more than 7 main sections in a web site
+ No more than 7 main menu items
+ No more than 7 items in between “spacers” in a menu
The rule of seven has other consequences for site design. Imagine a root, a home page. The site has seven main sections. The second level of the tree has seven navigation paths. If each section has seven sub-sections, then the third level has 49 navigation paths. If each sub-section has seven pages, the site has 343 navigation paths. Add up the series: 1 + 7 + 49 + 343 = 400. A conveniently ‘round’ number. As a rule-of-thumb, it provides a loose distinction between small and large sites. We contend tree-based navigation systems begin to fail on sites much larger than 400 categories. Large sites, larger data collections, need other navigation structures, such as searching and filtering.
**Wine Tree**
Let’s look at an example. Say, for instance, that we have a collection of wine, and that we organize it by Color, Region, and Price. A database could be of anything. It could be cars, for example, organized by Year, Type, and Make. It could be poems . . .
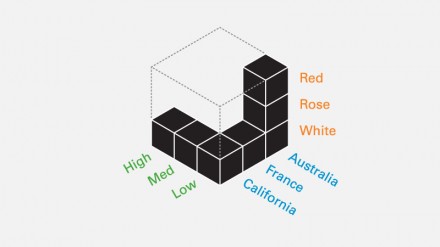
Each category has its own sub-categories: Color has Red, Rose, and White. Region has California, France, and Australia. Price has High, Medium, and Low.
In our example, the final result is a single bottle of wine that matches each of the categories. In a wine store, each category might have multiple bottles, e.g., from several vineyards and multiple years. Of course, vineyard and years are fourth and fifth dimensions. Variety of grape is another dimension. We’re keeping things simple for our illustration.
When we created our directory tree, we randomly started with Color, then chose Region, and finally Price. That order might make sense if we’re beginning our search with a goal of matching a wine to a food. However, we may want to begin with price or even region. The point is: No single taxonomy (tree structure) is best. Taxonomies are useful within a context—for a particular user, with a particular goal, at a particular time.
This set of information can be ordered in six ways (three unique elements in three positions yield six combinations).
1. ABC Price Region Color
2. ACB Price Color Region
3. BCA Region Color Price
4. BAC Region Price Color
5. CBA Color Region Price
6. CAB Color Price Region
Real data is often much richer, allowing even more combinations.
**Cube Structures**
Any one of the 6 trees is a valid representation of the data—and any one might be useful. How should we think about the data? Is there a more “natural” form?
In this case, the data has three dimensions. The data suggests a cube. We might say that its natural shape is a cube. Of course, a real database might have many more dimensions. While 4 or 5 or 6 or more dimensional spaces are difficult to represent, we can describe data spaces as N-dimensional—with the ability to be sliced or filtered along each dimension. The next section shows how that might work.
Using the same set of information as in our tree structure, we create the dimensions of the cube: Price is the first dimension. Region is the second dimension. Color is the third, and final dimension. This completes our wine collection.
We also know that each of our three dimensions has its own sub-categories: Price has High, Medium, and Low. Region has California, France, and Australia. Color has Red, Rose, and White. Adding these sub-categories divides our finished wine cube into 27 cells. Three cells make a row. Three rows make a block. Three blocks make up the cube.
Each leaf in the tree corresponds to a cell in the cube. Each cell has coordinates: x, y, z. 1,1,1 = Low, California, White. 3,3,3 = High, Australia, Red.
Re-ordering the dimensions provides the same six combinations as the tree structure.
1. Price, Region, Color
2. Price, Color, Region
3. Region, Color, Price
4. Region, Price, Color
5. Color, Region, Price
6. Color, Price, Region
**Possible Interfaces**
Now how would a user interact and navigate within this set of information? One could imagine a variety of interfaces to narrow down choices:
+ Column List
+ Pull-down Menus
+ Sliders
+ Checkboxes
**Pivoting**
Here’s where things get really interesting. The user has narrowed down to White, California, Low. But suppose she doesn’t like the results or she wants to explore other options. In a tree structure she would have to back out to the root and then travel back down the tree. Finding all the options for low cost would require an awful lot of climbing up and down the tree. The result would be a frustrated user.
The navigation solution involves two things. First, conceiving the data as an N-dimensional matrix and second recognizing that users may narrow along one path and then turn and “pivot” to expand back up another path—before narrowing again.
The accompanying PDF includes many diagrams which illustrate these concepts.